32bit整数型ハイレゾ音源登場。ところで「32bit整数型」って何？

数年前から量子化ビット数が32bitのハイレゾ音源データの販売が始まっています。また、DACやプレイヤーなどでも32bitの量子化ビット数に対応する機器が登場しています。

そんな中でe-onkyoが「32bit整数型」とわざわざ銘打ったハイレゾ音源の発売を開始しています。この「32bit整数型」とは一体何のことでしょう？

今回は32bit整数型のハイレゾ音源データに関して説明を行ないます。

パソコンでの32bit整数

32bit整数型ハイレゾ音源の説明を行なう前に、まずはパソコンなどデジタルな世界での数字の表現方法を説明する必要があります。ちょっと面倒なお話ですがご了承ください。

パソコンでは数字をすべて1か0かの2進数で表現しています。2進数32桁の情報量を32bitと言い表します。

32bit整数型というのは、2進数32桁を使って小数点を含まない整数を表す方式です。

通常のパソコンが扱う数字の場合にはプラスとマイナス両方を表現できないと都合が悪いので、パソコンで扱う32bit整数型は、マイナス2の31乗(-2,147,483,648)からゼロをはさんでプラスの2の31乗引く1(2,147,483,647)までを表すことが出来ます。

ハイレゾ音源の世界ではマイナスの数字が必要ありませんので、0から2の32乗引く1(4,294,967,295)までの範囲の整数を扱えるようになっています。細かくいうと、これは「符号なしの32bit整数」と呼んだりします。

もう一つの32bitで表現する数字の形式、浮動小数点

実は以前から販売されていた量子化ビット数32bitのハイレゾ音源データは、こちらの形式の数字が使われていました。「32bitの浮動小数点」の形式です。

こちらの形式では、名前に「浮動小数点」とあるとおりに、見かけ上小数点の位置があちこちに動き回ります。この部分は、今回のお話には関係ありませんので脇に置いておきます。

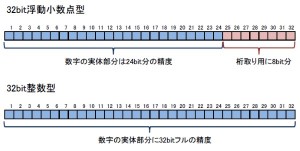
この形式の数字では、数字本体の部分を24bit、2進数24桁で表し、残りの8bit、2進数8桁を使って、桁数を表現しています。分かりやすく書くと、12345 x 10の5乗、みたいな表現の仕方をします。

桁取りに8bit使っていますので、桁部分では一般的には10のマイナス128乗から10の127乗までの範囲を表現できます。このため非常に小さな数から巨大な数までを表すことが出来るようになっています。

32bit浮動小数点型の問題点

この部分はハイレゾ音源でもパソコンで扱う数字においても同じことなのですが、32bit浮動小数点型では数字の「有効桁数」に当たる部分のデータは24bit分だけです。

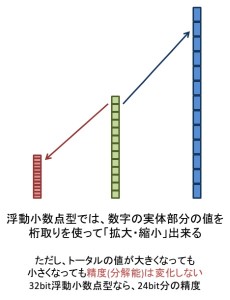
桁取りに当たる部分もフルに活用して全体として表現できる数字の幅を考えると極めて広い幅があるのですが、ある一つの数字だけで考えると、数字の「精度」は24bit分の精度しかない、ということです。

これをハイレゾ音源に焼き直して考えると、音楽全体としてのダイナミックレンジは極めて広大な幅を取ることが可能ですが、ある一瞬の音を切り出すと、その音の精度は量子化ビット数24bitの場合の分解能と変わらない、ということになります。

32bit整数型ではすべての瞬間の分解能が32bit分

これに対して32bit整数型のハイレゾ音源では、すべてのデータを数字本体に使っていて桁取りのためのデータがありません。ですので、すべての瞬間で32bit分の音のデータの精度が確保されています。

32bit整数型では音楽全体としてみた時のダイナミックレンジは限定されることになるはずですが、それでも192dbものダイナミックレンジが確保できます。通常、これほどの範囲のダイナミックレンジに対応できるアンプやスピーカー、イヤフォンなどは存在しませんので、十分な性能があると言えます。

32bit浮動小数点型のハイレゾ音源にも実は様々なメリットがあり、一概に32bit整数型が良い、とは言い切れない部分もあるのですが、こと再生に関しては、32bit整数型の方がより緻密な音楽の再現が出来る可能性があります。

そういう意味ではe-onkyoのアプローチは面白い試みだと思います。